Panduan Pengujian Hipotesis Dua Rata-Rata Beserta Contohnya
Hipotesis Statistik adalah pernyataan statistik tentang populasi yang diteliti. Jika menguji hipotesis penelitian dengan perhitungan statistik, maka rumusan hipotesis tersebut perlu diubah kedalam rumusan hipotesis statistik.
a). Untuk dan
dan 
b). Untuk dan
dan  ;
;
c). Untuk dan
dan 
a). Untuk
 dan
dan 
(1)diterima jika
(2)ditolak jika
b). Untuk
 dan
dan  ;
;(1)diterima jika
(2)ditolak jika
c). Untuk
 dan
dan 
(1)diterima jika

(2)ditolak jika
atau
Kalau dalam rumusan hipotesis penelitian hanya dituliskan salah satu saja yaitu hipotesis alternatif (Ha) atau hipotesis nol (Ho). Sedangkan dalam hipotesis statistik keduanya dipasangkan sehingga dapat diambil keputusan dengan tegas yaitu menerima Ho berarti menolak Ha begitu juga sebaliknya apabila Ho berarti menerima Ha. Hipotesis satistika dirumuskan untuk menjelaskan gambaran dan parameter apa dari populasi.
1. Jenis Pengujian Hipotesis
a. Hipotesis Direksional
Hipotesis Direksional adalah rumusan hipotesis yang arahnya sudah jelas atau disebut juga hipotesis langsung. Sedangkan pengujian hipotesis direksional terdiri dati dua yaitu uji pihak kiri dan uji pihak kanan.
b. Hipotesis Non Direksional
hipotesis non direksional (hipotesis tidak langsung) adalah hipotesis yang tidak menunjukan arah tertentu. Jika rumusan Ha berbunyi kalimat: tidak sama dengan (≠), maka sebaiknya Ho berbunyi kalimat: sama dengan(=). Pengujian ini menggunakan uji dua pihak (two tailed test).
UJI HIPOTESIS DUA RATA-RATA
Hipotesis adalah perumusan sementara mengenai sesuatu hal yang dibuat untuk menjelaskan hal itu dan untuk menuntun atau mengarahkan penelitian selanjutnya. Pengujian hipotesis berhubungan dengan penerimaan atau penolakan suatu hipotesis. Langkah atau prosedur untuk menentukan apakah menerima atau menolak hipotesis dinamakan pengujian hipotesis.
Untuk pengujian hipotesis, nilai-nilai statistik perlu dihitung kemudian dibandingkan menggunakan kriteria tertentu. Jika hasil yang didapat dari penelitian itu, dalam pengertian peluang, jauh berbeda dari hasil yang diharapkan terjadi berdasarkan hipotesis, maka hipotesis ditolak, jika terjadi sebaliknya hipotesis diterima (Sudjana, 1984:213).
A. Dua Tipe Hipotesis
· Hipotesis nihil/nol (H0) yaitu hipotesis yang menyatakan tidak adanya hubungan antara dua variabel atau lebih atau tidak adanya perbedaan antara dua kelompok atau lebih.
· Hipotesis alternatif (H1) yaitu hipotesis yang menyatakan adanya hubungan antara dua variabel atau lebih atau adanya perbedaan antara dua kelompok atau lebih
B. Dua Macam Kekeliruan
Dalam melakukan pengujian hipotesis, ada dua macam kekeliruan yang dapat terjadi, yaitu:
· Kekeliruan macam I: menolak hipotesis yang seharusnya diterima.
· Kekeliruan macam II: menerima hipotesis yang seharusnya ditolak
Untuk mengingat hubungan antara hipotesis, kesimpulan, dan macam kekeliruan dapat dilihat dalam tabel berikut.
Kesimpulan
|
Keadaan Sebenarnya
| |
Hipotesis Benar
|
Hipotesis Salah
| |
Terima hipotesis
|
Kekeliruan Macam II (β)
(kuasa uji = 1 – β)
| |
Tolak hipotesis
|
Kekeliruan Macam I
(taraf signifikan α)
| |
C. Arah Pengujian Hipotesis
Pengujian hipotesis dapat dilakukan secara uji satu pihak dan uji dua pihak.
1. Uji dua pihak
Uji dua pihak digunakan bila hipotesis nol (H0) berbunyi “sama dengan” dan hipotesis alternatifnya (Ha) berbunyi “tidak sama dengan”. Dalam distribusi statistik yang digunakan terdapat dua daerah kritis pada masing-masing ujung distribusi.
2. Uji Pihak Kanan
Uji pihak kanan digunakan apabila hipotesis nol (H0) berbunyi “lebih kecil atau sama dengan ( < )” dan hipotesis alternatifnya (Ha) berbunyi “lebih besar (>)”. Kalimat lebih kecil atau sama dengan sinonim dengan kata “paling besar”. Dalam distribusi yang digunakan terdapat sebuah daerah kritis yang letaknya di ujung di sebelah kanan. Luas daerah tersebut sama dengan

3. Uji pihak kiri
Uji pihak kanan digunakan apabila hipotesis nol (H0) berbunyi “lebih besar atau sama dengan ( > )” dan hipotesis alternatifnya (Ha) berbunyi “lebih kecil ( < )”. Kalimat lebih besar atau sama dengan sinonim dengan kata “paling sedikit atau paling kecil”. Sama hal nya dengan pihak kanan, dalam distribusi yang digunakan terdapat sebuah daerah kritis namun letaknya di ujung di sebelah kiri. Luas daerah tersebut sama dengan

D. Menguji Kesamaan Dua Rata-Rata : Uji Dua Pihak
Banyak penelitian yang memerlukan perbandingan antara dua keadaan atau tepatnya dua populasi. Misalkan kita mempunyai dua populasi normal masing-masing dengan rata-rata dan
dan sedangkan simpangan bakunya
sedangkan simpangan bakunya .
.
Dari populasi kesatu yang diambil sebuah sampel acak berukuran sedangkan dari populasi kedua sebuah sampel berukuran
sedangkan dari populasi kedua sebuah sampel berukuran dari kedua sampel ini berturut-turut didapat
dari kedua sampel ini berturut-turut didapat .
.
Akan diuji tentang rata-rata Pasangan hipotesis dan alternatif yang akan diuji adalah:
Pasangan hipotesis dan alternatif yang akan diuji adalah:
Untuk ini kita bedakan hal-hal berikut :

 dimana
dimana  didapat dari daftar normal baku dengan peluang
didapat dari daftar normal baku dengan peluang  .
.
2.
Jika H benar dan dimana
dimana  tidak diketahui harganya. Maka rumus statistik yang digunakan adalah:
tidak diketahui harganya. Maka rumus statistik yang digunakan adalah:

Dengan

Menurut teori distribusi sampling, maka statistik t di atas berdistribusi student dengan .Kriteria pengujian adalah : terima
.Kriteria pengujian adalah : terima  jika
jika  , dimana
, dimana  didapat dari daftar distribusi dengan
didapat dari daftar distribusi dengan  . dan peluang
. dan peluang  . Untuk harga t lainnya
. Untuk harga t lainnya  ditolak.
ditolak.
Jika kedua simpangan baku tidak sama tetapi kedua populasi berdistribusi normal, hingga sekarang belum ada statistik yang tetap yang dapat digunakan. Pendekatan yang cukup memuaskan adalah dengan menggunakan statistika sehingga rumus yang digunakan adalah sebagai berikut:
sehingga rumus yang digunakan adalah sebagai berikut:

Kriteria pengujian adalah : terima hipotesis jika
jika

Dengan :







 dan
dan 




 dan
dan sedangkan simpangan bakunya
sedangkan simpangan bakunya .
.Dari populasi kesatu yang diambil sebuah sampel acak berukuran
 sedangkan dari populasi kedua sebuah sampel berukuran
sedangkan dari populasi kedua sebuah sampel berukuran dari kedua sampel ini berturut-turut didapat
dari kedua sampel ini berturut-turut didapat .
. Akan diuji tentang rata-rata
 Pasangan hipotesis dan alternatif yang akan diuji adalah:
Pasangan hipotesis dan alternatif yang akan diuji adalah:Untuk ini kita bedakan hal-hal berikut :
1.  dan
dan  diketahui
diketahui
Statistik yang digunakan jika H benar, ialah :

Dengan taraf nyata  maka kriteria pengujian adalah terima
maka kriteria pengujian adalah terima  jika
jika
 maka kriteria pengujian adalah terima
maka kriteria pengujian adalah terima  jika
jika  dimana
dimana  didapat dari daftar normal baku dengan peluang
didapat dari daftar normal baku dengan peluang  .
.
2.  dan
dan  tidak diketahui
tidak diketahui
Jika H benar dan
 dimana
dimana  tidak diketahui harganya. Maka rumus statistik yang digunakan adalah:
tidak diketahui harganya. Maka rumus statistik yang digunakan adalah:
Dengan

Menurut teori distribusi sampling, maka statistik t di atas berdistribusi student dengan
 .Kriteria pengujian adalah : terima
.Kriteria pengujian adalah : terima  jika
jika  , dimana
, dimana  didapat dari daftar distribusi dengan
didapat dari daftar distribusi dengan  . dan peluang
. dan peluang  . Untuk harga t lainnya
. Untuk harga t lainnya  ditolak.
ditolak.
3.  dan kedua-duanya tidak diketahui
dan kedua-duanya tidak diketahui
Jika kedua simpangan baku tidak sama tetapi kedua populasi berdistribusi normal, hingga sekarang belum ada statistik yang tetap yang dapat digunakan. Pendekatan yang cukup memuaskan adalah dengan menggunakan statistika
 sehingga rumus yang digunakan adalah sebagai berikut:
sehingga rumus yang digunakan adalah sebagai berikut:
Kriteria pengujian adalah : terima hipotesis
 jika
jika 
Dengan :



didapat dari daftar distribusi student dengan peluang
dan dk = m. Untuk harga t lainnya, H ditolak.
4. Observasi berpasangan
Untuk observasi lapangan, kita ambil hipotesis dan hipotesis alternatifnya adalah :




Jika  maka data
maka data 
 maka data
maka data 
menghasilkan rata-rata  dan simpangan baku
dan simpangan baku  . Untuk pengujian hipotesis, gunakan rumus statistik:
. Untuk pengujian hipotesis, gunakan rumus statistik:
 dan simpangan baku
dan simpangan baku  . Untuk pengujian hipotesis, gunakan rumus statistik:
. Untuk pengujian hipotesis, gunakan rumus statistik:
dan terima H jika 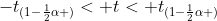 dimana
dimana  didapat dari daftar distribusi t dengan peluang
didapat dari daftar distribusi t dengan peluang  dan dk = (n - 1). Dalam hal lainnya H di tolak.
dan dk = (n - 1). Dalam hal lainnya H di tolak.
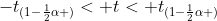 dimana
dimana  didapat dari daftar distribusi t dengan peluang
didapat dari daftar distribusi t dengan peluang  dan dk = (n - 1). Dalam hal lainnya H di tolak.
dan dk = (n - 1). Dalam hal lainnya H di tolak.E. Menguji Kesamaan Dua Rata-Rata : Uji Satu Pihak
Sebagaimana dalam uji dua pihak, untuk uji satu pihak pun dimisalkan bahwa kedua populasi berdistribusi normal dengan rata-rata 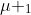 dan
dan  dan simpangan bakunya
dan simpangan bakunya  dan
dan  . Karena umumnya besar
. Karena umumnya besar  dan
dan  tidak diketahui, maka disini akan ditinjau hal-hal tersebut dimana
tidak diketahui, maka disini akan ditinjau hal-hal tersebut dimana  atau
atau  .
.
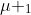 dan
dan  dan simpangan bakunya
dan simpangan bakunya  dan
dan  . Karena umumnya besar
. Karena umumnya besar  dan
dan  tidak diketahui, maka disini akan ditinjau hal-hal tersebut dimana
tidak diketahui, maka disini akan ditinjau hal-hal tersebut dimana  atau
atau  .
.
1. Uji Pihak Kanan
yang diuji adalah:


dalam hal ini  , maka statistik yang digunakan adalah statistik t dengan
, maka statistik yang digunakan adalah statistik t dengan  seperti rumus di atas. Kriteria pengujian yang berlaku adalah:
seperti rumus di atas. Kriteria pengujian yang berlaku adalah:
 , maka statistik yang digunakan adalah statistik t dengan
, maka statistik yang digunakan adalah statistik t dengan  seperti rumus di atas. Kriteria pengujian yang berlaku adalah:
seperti rumus di atas. Kriteria pengujian yang berlaku adalah:
Terima  jika
jika  dan tolak
dan tolak  jika t mempunyai harga lain.
jika t mempunyai harga lain.
 jika
jika  dan tolak
dan tolak  jika t mempunyai harga lain.
jika t mempunyai harga lain.
Jika  , maka rumus statistik yang digunakan adalah
, maka rumus statistik yang digunakan adalah  . Dalam hal ini kriteria yang digunakan adalah tolak
. Dalam hal ini kriteria yang digunakan adalah tolak  jika:
jika:
 , maka rumus statistik yang digunakan adalah
, maka rumus statistik yang digunakan adalah  . Dalam hal ini kriteria yang digunakan adalah tolak
. Dalam hal ini kriteria yang digunakan adalah tolak  jika:
jika:
dan terima  jika terjadi sebaliknya. Dimana :
jika terjadi sebaliknya. Dimana :
 jika terjadi sebaliknya. Dimana :
jika terjadi sebaliknya. Dimana : dan
dan 
2. Uji Pihak Kiri
yang diuji adalah:


Langkah yang ditempuh dalam hal ini sejalan dengan uji pihak kanan. Jika  dan kedua-duanya tidak diketahui, maka statistik yang digunakan adalah statistik t dengan
dan kedua-duanya tidak diketahui, maka statistik yang digunakan adalah statistik t dengan  seperti rumus di atas. Kriteria pengujian yang berlaku adalah:
seperti rumus di atas. Kriteria pengujian yang berlaku adalah:
 dan kedua-duanya tidak diketahui, maka statistik yang digunakan adalah statistik t dengan
dan kedua-duanya tidak diketahui, maka statistik yang digunakan adalah statistik t dengan  seperti rumus di atas. Kriteria pengujian yang berlaku adalah:
seperti rumus di atas. Kriteria pengujian yang berlaku adalah: tolakjika dan
dan terima
jika t mempunyai harga lain.
jika  , maka statistik yang digunakan adalah
, maka statistik yang digunakan adalah  . Dalam hal ini kriteria yang digunakan adalah tolak
. Dalam hal ini kriteria yang digunakan adalah tolak  jika:
jika:
 , maka statistik yang digunakan adalah
, maka statistik yang digunakan adalah  . Dalam hal ini kriteria yang digunakan adalah tolak
. Dalam hal ini kriteria yang digunakan adalah tolak  jika:
jika:
dan terima  jika terjadi sebaliknya.
jika terjadi sebaliknya.
 jika terjadi sebaliknya.
jika terjadi sebaliknya.
Dimana:

A. Contoh
Judul : Pengaruh Model Pembelajaran Kolaboratif Terhadap Hasil Belajar Matematika Siswa Kelas VIII Semester Ganjil SMP Negeri 1 Kelumbayan Barat Tanggamus Tahun Pelajaran 2012/2013.
Penulis : Tri Wahyudi
Tabel Daftar Nilai Tes Matematika Siswa
Kelas Eksperimen dan Kelas Kontrol
No.
|
Kelas Eksperimen
|
No.
|
Kelas Kontrol
|
1
|
63
|
1
|
53
|
2
|
77
|
2
|
53
|
3
|
63
|
3
|
57
|
4
|
47
|
4
|
40
|
5
|
70
|
5
|
40
|
6
|
57
|
6
|
50
|
7
|
60
|
7
|
73
|
8
|
77
|
8
|
57
|
9
|
60
|
9
|
40
|
10
|
80
|
10
|
43
|
11
|
67
|
11
|
60
|
12
|
73
|
12
|
63
|
13
|
73
|
13
|
50
|
14
|
67
|
14
|
47
|
15
|
93
|
15
|
47
|
16
|
83
|
16
|
50
|
17
|
80
|
17
|
67
|
18
|
57
|
18
|
60
|
19
|
57
|
19
|
70
|
20
|
73
|
20
|
67
|
21
|
47
|
21
|
53
|
22
|
50
|
22
|
60
|
23
|
50
|
23
|
77
|
24
|
70
|
24
|
43
|
25
|
60
|
25
|
63
|
26
|
83
|
26
|
87
|
27
|
53
|
27
|
63
|
28
|
90
|
28
|
50
|
29
|
60
|
29
|
50
|
30
|
73
|
30
|
83
|
31
|
80
|
31
|
53
|
32
|
70
|
32
|
67
|
33
|
53
|
33
|
53
|
34
|
50
|
34
|
53
|
35
|
70
|
35
|
73
|
36
|
60
|
36
|
70
|
37
|
93
|
37
|
77
|
38
|
77
|
38
|
53
|
39
|
63
|
39
|
70
|
40
|
70
|
Tabel distribusi frekuensi hasil tes pada kelas eksperimen
Nilai
|  |  |  |  |  |
47 – 54
55 – 62
63 – 70
71 – 78
79 – 86
 87 87 |
7
8
9
7
5
3
|
50,5
58,5
66,5
74,5
82,5
90,5
|
2550,25
3422,25
4422,25
5550,25
6806,25
8190,25
|
353,5
468
598,5
521,5
412,5
271,5
|
17851,75
27378
39800,25
38851,75
34031,25
24750,75
|
Jumlah
|
39
|
423
|
30941,5
|
2625,5
|
182483,75
|
Maka dapat dicari rata-rata  dan simpangan baku
dan simpangan baku  sebagai berikut:
sebagai berikut:
 dan simpangan baku
dan simpangan baku  sebagai berikut:
sebagai berikut:
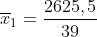

Simpangan bakunya adalah:







Daftar distribusi frekuensi hasil tes pada kelas kontrol.
Nilai
|  |  |  |  |  |
47 – 47
48 – 55
56 – 63
64 – 71
72 – 79
807
|
7
12
8
7
4
2
|
43,5
51,5
59,5
67,5
75,5
83,5
|
1892,25
2652,25
3540,25
4556,25
5700,25
6972,25
|
304,5
618
476
472,5
302
167
|
13245,75
31827
28322
31893,75
22801
13944,5
|
Jumlah
|
40
|
381
|
25313,5
|
2340
|
142034
|
Maka dapat dicari rata - rata (  ) dan simpangan baku (
) dan simpangan baku ( ) sebagai berikut:
) sebagai berikut:
 ) dan simpangan baku (
) dan simpangan baku ( ) sebagai berikut:
) sebagai berikut:


Simpangan bakunya adalah :







Pengujian Hipotesis
a). Uji Kesamaan Dua Rata - Rata : Uji Dua Pihak
Rumusan Hipotesis

Tidak ada perbedaan rata-rata hasil belajar matematika siswa yang menggunakan model pembelajaran kolaboratif dengan siswa yang menggunakan metode konvesional.
Ada perbedaan rata-rata hasil belajar matematika siswa yang menggunakan model pembelajaran kolaboratif dengan siswa yang menggunakan metode konvesional.
Kriteria Uji:
Terima  jika
jika  selain itu
selain itu  ditolak.
ditolak.
 jika
jika  selain itu
selain itu  ditolak.
ditolak.
Diketahui:




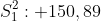

Dengan:

Dimana:




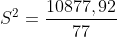
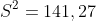


Harga S dimasukkan ke dalam rumus
 :
:





Dengan cara melihat tabel taraf signifikan 5%, yaitu :
 .Berdasarkan kriteria uji terima
.Berdasarkan kriteria uji terima Terima
 jika
jika  , maka
, maka  ditolak
ditolak  diterima.
diterima.Berarti ada perbedaan antara rata-rata hasil belajar matematika siswa yang menggunakan model pembelajaran kolaboratif dengan siswa yang menggunakan metode konvesional
b). Uji kesamaan dua rata-rata : Uji satu pihak
Rumusan hipotesis:

Rata-rata hasil belajar matematika siswa yang menggunakan model pembelajaran kolaboratif lebih rendah dari atau sama dengan rata-rata hasil belajar matematika siswa yang menggunakan metode pembelajaran konvensional.
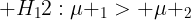
Rata-rata hasil belajar matematika siswa yang menggunakan model pembelajaran kolaboratif lebih tinggi dari rata-rata hasil belajar matematika siswa yang menggunakan metode pembelajaran konvensional.





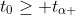







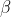

0 Response to "Uji Hipotesis Kesamaan Dua Rata-Rata"
Posting Komentar