Anova Two Way

Anova Two Way

Two-Way Anova disebut juga dengan Anova 2 Arah atau Analisis Varian 2 Faktor.

ANOVA dua arah membandingkan perbedaan rata-rata antara kelompok yang telah dibagi pada dua variabel independen (disebut faktor). Anda perlu memiliki dua variabel independen berskala data kategorik dan satu variabel terikat berskala data kuantitatif/numerik (interval atau rasio).

Anova merupakan singkatan dari "analysis of varian" adalah salah satu uji komparatif yang digunakan untuk menguji perbedaan mean (rata-rata) data lebih dari dua kelompok. Ada dua jenis Anova, yaitu analisis varian satu faktor (one way anova) dan analisis varian dua faktor (two ways anova). Pada artikel ini hanya akan dibahas analisis varian dua faktor.

Untuk melakukan uji Anova, harus dipenuhi beberapa asumsi, yaitu:

1. Sampel berasal dari kelompok yang independen
2. Varian antar kelompok harus homogen
3. Nilai Residual berdistribusi normal (Pelajari juga tentang uji normalitas)

Berikut akan kami jelaskan tutorial Two Way Anova dalam SPSS.

Kita ambil contoh penelitian yang berjudul "Pengaruh Gender dan Pendidikan Terhadap Nilai Ujian Fisika".

Agar lebih mudah, sebaiknya gunakan dalam uji coba berikut:

Langkah pertama adalah siapkan dulu data sebagai berikut:

Two Way Anova Dataset Excel

• Buka Aplikasi SPSS For Windows
• Buka Tab Variable View: Buat 3 variabel dengan ketentuan sebagai berikut: 

·         Variabel independen: 1. "Gender" dengan kategori Pria dan Wanita. Measure Nominal, Decimals=0, Type Numeric dan isi value: 1= Pria, 2=Wanita. 

·         Variabel independen: 2. "Pendidikan" dengan kategori SLTP, SLTA dan PT. Measure Nominal, Decimals=0, Type Numeric dan isi value: 1= SLTP, 2=SLTA, 3=PT.

·         Variabel dependen: "Ujian", Decimals=0, Measure Scale, Type Numeric.

Two Way Anova Dataview

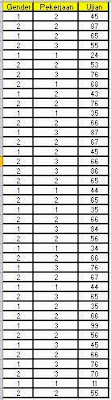
• Buka Tab Data View: Isi data seperti di bawah ini:

Two Way Anova Dataset

• Setelah data terisi, pada menu, Klik Analyze, General Linear Model, Univariate. Maka akan mucul jendela sbb: Masukkan Ujian ke kotak Dependent Variable, masukkan Gender dan Pendidikan ke kotak Fixed factor(s). (Kotak Random factor (s) dan Covariate(s) tidak akan kita gunakan dalam Two Ways Anova, kotak tersebut akan digunakan pada "Uji Ancova").

Two Way Anova SPSS Proses

• Klik Plot, maka akan muncul jendela seperti di bawah ini: Masukkan Gender  ke kotak Horizontal Axis dan Pendidikan ke kotak Separate Lines. 

Two Way Anova SPSS Plot

• Klik Add, maka akan tampak sbb:

Two Way Anova SPSS Plot Continue

• Klik Continue.
• Klik Post Hoc, maka muncul jendela sbb: Masukkan Pendidikan ke kotak Post Hoc Test for. Centang Tukey

Two Way Anova SPSS Post Hoc

• Klik Continue
• Klik Options, maka akan muncul jendela sbb: Masukkan Gender, Pendidikan, dan Gender*Pendidikan ke dalam kotak Display Means for. Pada Display centang Descriptive statistics dan Homogentity test.

Two Way Anova SPSS Homogenity

• Klik Continue
• Klik OK
• Lihat Hasil!

Dari tabel di atas, kita bisa menilai rata-rata nilai ujian berdasarkan gender dan pendidikan. sebagai contoh: nilai rata-rata ujian pria dengan pendidikan SLTP sebesar 32,43 sedangkan nilai ujian wanita yang berpendidikan SLTA sebesar 65,13 dan begitu seterusnya.

Di bawah ini adalah Tabel Levene's Test. Digunakan untuk menilai homogenitas tiap variabel.

Di atas menunjukkan nilai (Signifikansi) Sig. 0,527 di mana > 0,05 sehingga bisa dikatakan varian antar group berbeda secara signifikan.

Tabel di bawah ini menunjukkan hasil dari uji Two Way Anova:

Dari tabel di atas, kita mendapatkan nilai-nilai penting yang bisa disimpulkan sebagai berikut:

1. Corrected Model: Pengaruh Semua Variabel independen (Gender, Pendidikan dan Interaksi gender dengan pendidikan atau "Gender*Pendidikan") secara bersama-sama terhadap variabel dependen (Nilai Ujian). Apabila Signifikansi (Sig.) < 0,05 (Alfa) = Signifikan. Contoh di atas 0,000 berarti model valid.
2. Intercept: Nilai perubahan variabel dependen tanpa perlu dipengaruhi keberadaan variabel independen, artinya tanpa ada pengaruh variabel independen, variabel dependen dapat berubah nilainya. Apabila Signifikansi (Sig.) < 0,05 (Alfa) = Signifikan. Contoh di atas 0,000 berarti intercept signifikan.
3. Gender: Pengaruh gender terhadap nilai ujian di dalam model. Apabila Signifikansi (Sig.) < 0,05 (Alfa)= Signifikan. Contoh di atas 0,005 berarti gender berpengaruh signifikan.
4. Pendidikan: Pengaruh pendidikan terhadap nilai ujian di dalam model. Apabila Signifikansi (Sig.) <0 0="" atas="" berarti="" berpengaruh="" di="" lfa="" li="" nbsp="" ontoh="" pendidikan="" signifikan.="">
5. Gender*Pendidikan: Pengaruh Gender*pendidikan terhadap nilai ujian di dalam model. Apabila Signifikansi (Sig.) <0 0="" atas="" berarti="" berpengaruh="" di="" gender="" lfa="" li="" nbsp="" ontoh="" pendidikan="" signifikan.="">
6. Error: Nilai Error model, semakin kecil maka model semakin baik.
7. R Squared: Nilai determinasi berganda semua variabel independen dengan dependen. Contoh di atas 0,668 di mana mendekati 1, berarti korelasi kuat.

Dari 7 kesimpulan di atas, dalam uji Two Way Anova, poin 1, 3, 4 dan 5 adalah yang terpenting (tanpa mengabaikan yang lain).

Tabel di bawah ini adalah Tabel Tukey Post Hoc digunakan untuk menilai kategori manakah dari variabel pendidikan yang memiliki perbedaan signifikan:

Yang ada perbedaan signifikan ditandai dengan tanda bintang (*). Dari tabel di atas, semuanya ditandai dengan bintang, berarti  semuanya ada perbedaan yang signifikan.

Diagram Plot di bawah ini berguna untuk menilai apakah ada interaksi efek antar variabel. Namun diagram ini tidak bisa dijadikan bahan acuan yang valid. Tetapi hanya sekedar memberikan gambaran saja. Apabila garis-garis tidak menunjukkan kesejajaran, maka dicurigai ada efek interaksi.

Diagram di atas menunjukkan ada ketidak sejajaran garis, maka dicurigai ada efek interaksi.